เอกนาม
เอกนาม
คือ จำนวนที่เขียนในรูปการคูณของค่าคงที่กับตัวแปรตั้งแต่ 1 ตัวขึ้นไป
โดยที่เลขชี้กำลังของตัวแปรแต่ละตัว เป็น ศูนย์หรือจำนวนเต็มบวก
จำนวนที่เป็นเอกนาม เช่น 5X3Y
, 3-2AB , ab2c3 , 7
|
|
จำนวนที่ไม่ใช่เอกนาม เช่น 4X-3Y
, n + 6 , 2a/3b
|
ดังนั้น เอกนามมี 2 ส่วน คือ
1.
ค่าคงที่ เรียกว่า สัมประสิทธิ์ของเอกนาม
2.
ส่วนที่อยู่ในรูปการคูณของตัวแปร
โดยเลขชี้กำลังของตัวแปร แต่ละตัวเป็นศูนย์ หรือจำนวนเต็มบวก
เรียกผลบวกของเลขชี้กำลัง ของตัวแปรทั้งหมดในเอกนามว่า ดีกรีของเอกนาม
เช่น 78X2Y3Z ดีกรี คือ 6
( เลขชี้กำลังของ X คือ 2 , Y คือ 3 , Z คือ 1 ) และสัมประสิทธิ์คือ
78
แต่เอกนาม
0 จะบอกได้ไม่แน่นอน
เนื่องจาก 0 = 0Xn โดยที่ X ไม่เท่ากับศูนย์ และ n เป็นจำนวนเต็มบวกหรือศูนย์
ดังนั้น ไม่กล่าวถึงดีกรีของ 0
การบวก-ลบ
เอกนาม
เอกนามที่คล้ายกันสามารถนำมาบวกลบกันได้โดยสมบัติแจกแจง ดังนี้
3XY4 + 7XY4 = (3+7)XY4 ผลบวกของเอกนามคล้ายเท่ากับ
(ผลบวกของสัมประสิทธิ์)ตัวแปรชุดเดิม
|
|
3XY4 - 7XY4 = (3-7)XY4 ผลลบของเอกนามคล้ายเท่ากับ (ผลลบของสัมประสิทธิ์) ตัวแปรชุดเดิม
|
กรณีที่เอกนามไม่คล้ายกันให้เขียนผลบวกในรูปเดิม
เช่น 7X4Y + 7XY4 ผลลัพธ์คือ 7X4Y + 7XY4
การแยกตัวประกอบของพหุนาม
http://www.myfirstbrain.com/student_view.aspx?ID=83868
การแยกตัวประกอบพหุนามดีกรีสอง ในรูปผลต่างกำลังสอง A2 - B2 = (A – B) (A + B)
http://www.myfirstbrain.com/student_view.aspx?ID=83866
การแยกตัวประกอบ
ข้อมูลจากวิกิพีเดีย สารานุกรมเสรี
การแยกตัวประกอบ (อังกฤษ: factorization) ในทางคณิตศาสตร์ หมายถึง การแบ่งย่อยวัตถุทางคณิตศาสตร์ (เช่น จำนวน พหุนาม หรือเมทริกซ์)
ให้อยู่ในรูปผลคูณของวัตถุอื่น ซึ่งเมื่อคูณตัวประกอบเหล่านั้นเข้าด้วยกันจะได้ผลลัพธ์ดังเดิม
ตัวอย่างเช่น จำนวน 15 สามารถแยกตัวประกอบให้เป็นจำนวนเฉพาะได้เป็น 3 × 5
และพหุนาม 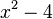 สามารถแยกได้เป็น
สามารถแยกได้เป็น  เป็นต้น
เป็นต้น
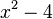 สามารถแยกได้เป็น
สามารถแยกได้เป็น  เป็นต้น
เป็นต้น
จุดมุ่งหมายของการแยกตัวประกอบ คือ การลดทอนวัตถุให้เล็กลง
อาทิ จากจำนวน ไปเป็น จำนวนเฉพาะ
จากพหุนาม ไปเป็น พหุนามลดทอนไม่ได้ (irreducible polynomial)
การแยกตัวประกอบจำนวนเต็มเป็นส่วนหนึ่งของทฤษฎีบทมูลฐานของเลขคณิต
ส่วนการแยกตัวประกอบพหุนามเป็นส่วนหนึ่งของทฤษฎีบทมูลฐานของพีชคณิต
สำหรับพหุนาม สิ่งที่ตรงข้ามกับการแยกตัวประกอบ คือ การกระจายพหุนาม (polynomial expansion) ซึ่งเป็นการคูณตัวประกอบทุกตัวเข้าด้วยกันเป็นพหุนามใหม่
การแยกตัวประกอบพหุนามกำลังสอง
พหุนามกำลังสองใดๆ บนจำนวนเชิงซ้อน (คือพหุนามที่อยู่ในรูป 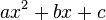 เมื่อ
เมื่อ  ) สามารถแยกตัวประกอบให้เป็นนิพจน์ที่อยู่ในรูป
) สามารถแยกตัวประกอบให้เป็นนิพจน์ที่อยู่ในรูป  เมื่อ
เมื่อ  และ
และ  คือรากของพหุนาม ซึ่งคำนวณได้จากสูตรกำลังสองดังนี้
คือรากของพหุนาม ซึ่งคำนวณได้จากสูตรกำลังสองดังนี้
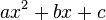 เมื่อ
เมื่อ  ) สามารถแยกตัวประกอบให้เป็นนิพจน์ที่อยู่ในรูป
) สามารถแยกตัวประกอบให้เป็นนิพจน์ที่อยู่ในรูป  เมื่อ
เมื่อ  และ
และ  คือรากของพหุนาม ซึ่งคำนวณได้จากสูตรกำลังสองดังนี้
คือรากของพหุนาม ซึ่งคำนวณได้จากสูตรกำลังสองดังนี้พหุนามที่สามารถแยกได้บนจำนวนเต็ม
บางครั้งพหุนามกำลังสองสามารถแยกออกได้เป็นทวินาม (binomial) สองตัวด้วยสัมประสิทธิ์ที่เป็นจำนวนเต็ม โดยไม่จำเป็นต้องใช้สูตรกำลังสองในการคำนวณ ซึ่งมีประโยชน์สำหรับการหารากของสมการกำลังสอง โดยที่พหุนาม
สามารถแยกได้เป็น
เมื่อ
จากนั้นจึงให้ทวินามแต่ละตัวเท่ากับศูนย์ แล้วคำนวณหาค่าของ x เพื่อหารากของสมการกำลังสอง
ไตรนามกำลังสองสมบูรณ์
พหุนามกำลังสองบางชนิดสามารถแยกตัวประกอบออกได้เป็นทวินามที่เหมือนกัน พหุนามนั้นเรียกว่า ไตรนามกำลังสองสมบูรณ์ หรือเพียงแค่ กำลังสองสมบูรณ์ ซึ่งพหุนามดังกล่าวสามารถแยกได้ดังนี้
ผลบวกและผลต่างกำลังสอง
ดูบทความหลักที่: ผลต่างกำลังสอง
การแยกตัวประกอบทางพีชคณิตอีกอย่างหนึ่งเรียกว่า ผลต่างกำลังสอง มีสูตรดังนี้
ซึ่งเป็นจริงสำหรับทั้งสองพจน์ ไม่ว่าจำนวนเหล่านั้นจะเป็นกำลังสองสมบูรณ์หรือไม่ ถ้าพจน์ทั้งสองลบกัน ก็ให้แทนด้วยสูตรดังกล่าวได้ทันที แต่ถ้าพจน์ทั้งสองบวกกัน ทวินามที่ได้จากการแยกตัวประกอบจะต้องมีจำนวนจินตภาพเข้ามาเกี่ยวข้อง ซึ่งแสดงได้ดังนี้
ตัวอย่างเช่น  สามารถแยกได้เป็น
สามารถแยกได้เป็น  เป็นต้น
เป็นต้น
 สามารถแยกได้เป็น
สามารถแยกได้เป็น  เป็นต้น
เป็นต้นการแยกตัวประกอบพหุนามอื่น ๆ[แก้]
ผลบวกและผลต่างกำลังสาม[แก้]
สูตรสำหรับการแยกตัวประกอบของผลบวกและผลต่างกำลังสามเป็นดังนี้ ผลบวกสามารถแยกตัวประกอบเป็น
และผลต่างสามารถแยกตัวประกอบเป็น
เช่น x3 − 103 (or x3 − 1000) สามารถแยกตัวประกอบเป็น (x − 10)(x2 + 10x + 100)
ศึกษาเพิ่มเติม..
เรื่อง การบวก ลบ เอกนาม และพหุนามและคูณหาร ค่าคงที่กับเอกนามและพหุนาม
|
ผลการเรียนรู้ที่คาดหวัง 1. สามารถบวกลบเอกนามได้
2. สามารถคูณ หาร เอกนามได้
3. สามารถบวกลบพหุนามได้
|
เอกนามคือ นิพจน์ที่สามารถเขียนให้อยู่ในรูปการคูณของค่าคงตัวกับตัวแปร ตั้งแต่หนึ่งตัว
ขึ้นไปโดยที่เลขชี้กำลังของตัวแปรแต่ละตัวเป็นศูนย์ หรือจำนวนเต็มบวก
นิพจน์ต่อไปนี้ทุกพจน์เป็นเอกนาม
3x , -4x
เอกนามประกอบด้วย 2 ส่วน คือส่วนที่เป็นค่าคงตัวและส่วนที่เป็นตัวแปร ซึ่งอยู่ในรูป
การคูณค่าคงตัว เรียกส่วนที่เป็นค่าคงตัวว่า สัมประสิทธิ์ของเอกนาม เรียกผลบวกของกำลัง
ของตัวแปรว่าดีกรี ของเอกนาม
เอกนามที่คล้ายกัน
เอกนาม 2 เอกนามจะคล้ายกันก็ต่อเมื่อ
1. เอกนามทั้งสองมีตัวแปรชนิดเดียวกัน
2. เลขชี้กำลังของตัวแปรตัวเดียวกันในแต่ละเอกนามเท่ากัน
เช่น 8Xy คล้ายกับ –5xy 6x2y คล้ายกับ
การบวก และการลบเอกนาม
เอกนามจะบวกลบกันได้ก็ต่อเมื่อเป็นเอกนามคล้าย
การบวกเอกนาม ผลบวกของเอกนามที่คล้ายกันคือเอาสัมประสิทธิ์บวกกัน ส่วนที่เป็นตัวแปรคงเดิม
เช่น 3x + 6X = 9X
+8x + 3X = 11x
3x2y + 5x2y = 8x2y
การลบเอกนามทำเหมือนการบวก
-6x + 8x = 2X
-3x – 5X = -8x
|
พหุนามคือ นิพจน์ที่อยู่ในรูปเอกนามหรือรูปผลบวกหรือผลลบของเอกนาม ตั้งแต่ 2 เอกนามขึ้นไปเช่น
5x3 + 4x2 – 7X + 1 เป็นพหุนาม ที่มี 4 พจน์
3x2 + 1 เป็นพหุนาม ที่มี 2 พจน์
การบวกและการลบพหุนามทำได้โดยตั้งบวกกันธรรมดา เรียงลำดับพจน์ที่มีเลขชี้กำลังมาก
ไปหาพจน์ทีมีเลขชี้กำลังน้อย แล้วจึงบวกลบที่มีตัวแปรเหมือนกัน และกำลังของตัวแปรเท่ากัน เช่น
1. (5x2 + 3x) + ( 6x2 - 4x) = (5x2 + 6x2) + ( 3x + (- 4x)
= 11 x2 + (-x)
= 11 x2 - x
2. (3x2 - 1) - (2 x2 + 3x) = (3 x2 – 2x2) - 1 - (3x)
= x2 – 3x - 1
|
การคูณเอกนามหรือพหุนามด้วยค่าคงที่
การคูณหรือหารเอกนามด้วยค่าคงที่ ให้นำค่าคงที่คูณกันได้เลย ส่วนตัวแปรเหมือนเดิม
- 3 ( 4x) = -12 x
8 (-6x) = -48 x
-2 ( -3 x) = + 6x
การคูณค่าคงที่กับพหุนาม ให้นำค่าคงที่คูณพหุนามทุกพจน์ เช่น
3 (4x + 8) = 12x + 24
-4 (x – 5) = - 4x +20
|
ตัวประกอบของพหุนามมีอยู่ทั้งหมด 8 รูปแบบด้วยกัน ซึ่งแต่ละรูปแบบก็จะมีวิธีในการแยกตัวประกอบที่คล้ายกันบ้าง ไม่คล้ายกันบ้าง แล้วแต่วิธี ส่วนรูปแบบต่างๆจะมีลักษณะดังนี้
การแยกตัวประกอบของพหุนามทั้ง 8 รูปแบบ
รูปแบบที่1: สมบัติการแจกแจง
หรือการดึงตัวร่วมออกมา เป็นวิธีที่ง่ายที่สุดในการแยกตัวประกอบของพหุนาม
ab + ac = a(b+c)
ตัวอย่าง: 3x2 + 6x = 3x(x+2)
รูปแบบที่2: พหุนามสองวงเล็บ
คือการแยกตัวประกอบออกมาเป็นสองวงเล็บที่คูณกันอยู่ พหุนามแบบสองวงเล็บนี้จะมีตั้งแต่ง่ายไปจนถึงยาก
x2 + 9x + 14 =0
ตัวอย่าง: (x+2) ( x+7) =0
รูปแบบที่3: พหุนามผลต่างกำลังสอง
รูปแบบนี้จะดูได้ง่ายมาก และสามารถใช้สูตรเพียงสูตรเดียวในการแยกตัวประกอบออกมาได้เลย
หน้า2 – หลัง2 = (หน้า-หลัง) (หน้า+หลัง)
ตัวอย่าง: x2 – 42 = 0
รูปแบบที่4: พหุนามกำลังสองสมบูรณ์
มีอยู่สองรูปแบบย่อยที่ต่างกันเพียงเครื่องหมาย +- ที่เดียวเท่านั้น ใช้สูตรในการแยกตัวประกอบ
น2 + 2นล + ล2 = (น+ล) (น+ล) = (น+ล)2
น2 – 2นล + ล2 = (น-ล) (น-ล) = (น-ล)2
รูปแบบที่5: พหุนาม แบบเพิ่มเข้า ลบออก
ใช้ในการแก้สมการพหุนามที่ไม่สามารถแก้ได้ในตอนแรก เราจะใช้หลักการใส่ตัวแปรเพิ่มเข้าไป หรือลบตัวแปรออกมา ทำให้สมการพหุนามใหม่มีรูปแบบที่ตรงกับรูปแบบอื่นและสามารถแยกตัวประกอบได้
รูปแบบที่6: พหุนาม ผลบวกและผลต่างกำลังสาม
มีอยู่สองรูปแบบที่ต่างกันที่เครื่องหมาย +- แต่เมื่อแยกตัวประกอบออกมาแล้ว สมการจะยาวหน่อยนึง
น3 + ล3 = (น + ล) (น2 – นล + ล2)
น3 – ล3 = (น – ล) (น2 + นล + ล2)
น3 – ล3 = (น – ล) (น2 + นล + ล2)
รูปแบบที่7: พหุนามแบบจับคู่
ใช้ความรู้จากรูปแบบที่ 1 มาช่วย โดยเริ่มจากการจับคู่ให้พหุนามก่อน บางครั้งต้องเรียงตำแหน่งใหม่ด้วย
ac + bc + ad + bd = (ac + bc) + (ad + bd) = c(a+b) + d(a+b) = (a+b) (c+d)
รูปแบบที่8: การหารสังเคราะห์
รูปแบบสุดท้ายที่สามารถแก้สมการพหุนามได้แทบจะทุกรูปแบบ แต่ว่าต้องแลกกับวิธีการทำที่ค่อยข้างยากและยาวเอาเรื่อง ส่วนใหญ่หลายคนทำผิดเพราะว่าบวกลบเลขผิดในขั้นตอนตรงกลาง การหารสังเคราะห์นี้สามารถใช้แก้สมการพหุนามดีกรีสูงๆตั้งแต่ x4 x3 ได้หมดเลย














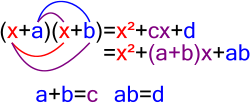













ไม่มีความคิดเห็น:
แสดงความคิดเห็น